Pourquoi les projections icosaédriques ont tendance à nous fasciner


Vous n'avez peut-être pas remarqué, mais la carte choisie pour illustrer la page d'accueil du blog Cartographie(s) numérique(s) est un extrait de la projection Fuller. Ce choix n'est pas dû au hasard. Cette projection cartographique n'a ni Nord ni Sud, ni haut ni bas, ni centrage ni cadrage prédéfinis. C'est que la projection Fuller est une projection icosaédrique. Explications...

Un icosaèdre est une forme particulière de polyèdre avec 20 triangles équilatéraux de même dimension (εἴκοσι en grec voulant dire vingt). Depuis l'Antiquité, cette figure fascine pour ses propriétés géométriques. L'idée ingénieuse de Richard Buckminster Fuller est d'avoir projeté des morceaux de terre sur ces 20 faces. Cet architecte était spécialiste des structures préfabriquées permettant de construire des bâtiments sphériques à partir d’éléments plans. On lui doit les premiers dômes géodésiques comme les boules géantes de Bâton Rouge (1958) ou celle du pavillon des États-Unis à l’exposition universelle de Montréal (1967). En 1954, Fuller met au point après plusieurs années de travail cette projection dite Dymaxion, contraction de « Dynamic maximum tension ».

L'avantage de cette projection est de subir très peu de distorsions. Cette carte, issue d’un travail à partir d’images satellites, unifie tous les pays en une seule île au milieu d’un vaste océan. Selon l’auteur, « ce planisphère rassemble tous les continents dans un ensemble sans discontinuité comme les astronautes peuvent voir la Terre de leur vaisseaux spatiaux. Il aide les hommes à prendre conscience que la planète est un système interdépendant ». En élaborant cette projection, Fuller ouvrait une nouvelle voie. La recherche de la projection parfaite respectant les contours et les surfaces n'a cessé en effet de préoccuper les cartographes depuis des décennies comme en atteste la mise au point de la toute récente projection Equal Earth.

Ce planisphère implique une perception de lecture universelle, sans hiérarchisation des terres émergées. Un peu comme dans un blog, la projection Fuller n'indique pas de sens de lecture. Ce qui ne veut pas dire qu'elle ne nécessite pas des pistes pour être décryptée. Fuller a en effet disposé ces 20 triangles de manière particulière afin de ne pas avoir à scinder les continents. Sur sa projection, l'Eurasie est reliée à l'Amérique par l'océan Arctique. Mais on peut imaginer d'autres découpages. Pour éviter ces discontinuités, Hellerick a proposé récemment une projection inspirée de la Buckminster Fuller, mais réduite à trois axes.



Depuis la projection Fuller de 1954, beaucoup d'autres projections polyédriques ont été mises au point. Le site Lynceans.org en donne des exemples et montre comment les projections utilisant des polyèdres ont permis d'améliorer la cartographie en évitant les déformations. Les possibilités de produire des projections en myriaèdres deviennent désormais quasi infinies avec l'aide des ordinateurs (à découvrir sur le site Myriahedral Projections). La page Unfolding the Earth présente les mille et unes façons de déplier la Terre avec des exemples et une vidéo très belle et efficace. Les cartes reproduites ci-dessous en montrent quelques exemples parmi d'autres. Outre les nombreux découpages qu'elles permettent, on peut remarquer que ces cartes n'ont pas de centre ni vraiment de bords. Comme le rappelle Christian Grataloup sur le blog Histoire globale,  il ne faut jamais oublier qu'à la différence de toute carte plane, la Terre n'a pas de bord. En voici une très bonne illustration avec ces cartes polyédriques dont les franges bleues des océans donnent une impression d'infinitude.




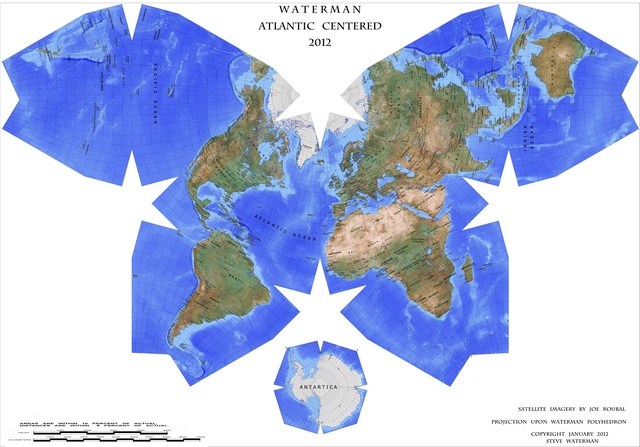
Une projection polyédrique intéressante et de plus en plus utilisée est la projection de Waterman (1996). Elle correspond à un octaèdre, elle s'inspire de l'ancienne projection de Cahill (1909) dite "en papillon" elle-même modifiée sous la forme de la projection Cahill-Keyes (1975). La projection de Waterman minimise les coupures entre grandes masses continentales et permet de représenter la Terre reliée par un océan unique. Elle est souvent utilisée pour représenter la globalisation du monde : voir par exemple l'Atlas de Sciences Po 2018 qui recourt largement à la projection Waterman.

 


Boris Müller donne des conseils pour construire soi-même une carte esthétique à partir d'une projection Waterman en papillon.

Dans cette quête permanente pour trouver la projection sinon la plus parfaite, du moins celle qui comporte le moins de déformations, de nouvelles voies ont été explorées depuis ces dernières décennies. La carte d'Hajime Narukawa (créée en 1999, mais vraiment connue à partir de 2016) est une tentative pour donner une représentation aussi fidèle que possible de la Terre. Cet architecte japonais (encore un architecte !) a repris la projection de Fuller et l'a divisée en 96 triangles. Il a pu en faire une espèce de pyramide (un tétraède) et ensuite un rectangle – des étapes nécessaires pour conserver la plus grande précision possible dans les rapports entre les masses continentales (voir sur le site japonais Géopalette). Nurakawa a baptisé cette carte Autagraph World Map, elle est consultable sur le site Autagraph. Le découpage met l'océan Pacifique au centre, mais de fait cette carte peut avoir d'autres centres. Hajime Narukawa insiste sur le fait que les changements climatiques rendent nécessaire une visualisation différente de la planète. Un des faits les plus intéressants, c’est d’inverser le rapport terre/mer. On voit un grand océan au milieu duquel surnagent des continents dont on perçoit beaucoup plus l’unité. La carte est téléchargeable au format PDF ou AI.


Les projections icosaédriques ont mobilisé les scientifiques et les cartographes. Elles ont aussi inspiré les artistes. La production artistique Earth Puzzle repose sur une représentation de la Terre sous forme de puzzle. La méthode a consisté à projeter la Terre sur un icosaèdre, puis à découper cette projection en 442 pièces de manière à montrer un agencement des continents et des océans sans orientation nord-sud et sans bordures véritables (cf liseré très découpé des côtes). Chaque pièce peut être connectée aux autres, ouvrant un nombre infini de possibilités pour représenter le monde. Le résultat est aussi esthétique que symbolique, les pièces de puzzle représentant elles-mêmes des formes animales.


La méthode pour projeter la sphère sur l’icosaèdre repose sur la technique des barycentres utilisée sur des triangles en géométrie plane mais transposée en géométrie sphérique (les explications sont données sur le site). Plusieurs modes de découpage sont donc possibles en fonction de la manière de disposer les 20 triangles. En voici quelques exemples, le but étant de donner des représentations multiples sans cadrage fixe :



Une belle animation accompagne la présentation de cette carte sur le site Nervous System.



Et pour finir sur une note d'humour, nous vous conseillons de lire ce billet sur le blog "Monde géonumérique" Ce que les projections disent de vous.


Prolongements

La publication du magazine Life a largement contribué à la diffusion de la projection Fuller avec son numéro du 1er mars 1943 : Life presents R. Buckminster Fuller's Dymaxion world. Le magazine donnait à ses lecteurs une méthode d'assemblage pour la réaliser à partir de feuilles de papier. Avec en prime, des polyèdres en couleurs prêt à découper ! A l'époque, Fuller n'est pas encore parvenu à trouver un découpage complètement satisfaisant qui ne scinde pas les continents. Il mettra plusieurs années avant d'y parvenir. En 1946, il fait breveter sa première version qui repose sur un cuboctaèdre (polyèdre à 14 faces régulières, dont 8 sont des triangles équilatéraux et 6 des carrés).

C'est seulement en 1954 que Fuller parvient à la version que nous connaissons qui repose sur un icosaèdre (polyèdre régulier constitué de 20 triangles). Parmi les découpages proposés dans le magazine Life, l'un d'entre eux met en valeur la zone Pacifique. Dans le contexte de la 2e Guerre mondiale, le magazine ne peut s'empêcher d'y voir "la logique impitoyable de l'impérialisme japonais". Pas sûr que cette vision ait plu à Fuller qui souhaitait que sa projection, formée de 5 continents réunis au sein d'un seul océan, puisse contribuer à la communication et la collaboration entre les peuples et les nations.



Dans les années 1960, Buckminster Fuller a proposé un jeu de simulation dénommé "jeu de la paix mondiale" (abrégé plus tard en World game) afin de faciliter une approche globale des problèmes. Ce jeu, qui repose sur des stratégies de résolution de problème obligeant les Etats-nations à trouver des solutions à l'échelle mondiale, utilise sa projection. Il est consultable en ligne sur le site Our World.

Lors du 70e anniversaire de la projection Fuller en 2013, le Buckminster Fuller Institute a lancé un concours invitant cartographes et artistes à s'en inspirer et à renouveler les formes, couleurs et supports de cette projection :
http://www.bfi.org/about-bfi/what-we-do/exhibitions/dymax-redux

Nicholas Felton, artiste-designer, a choisi la projection Fuller pour rendre compte de son expérience personnelle où le temps, à savoir les événements de sa vie durant toute une année, sont représentés comme des distances sur la carte :
http://feltron.com/FAR08.html

Aujourd'hui la projection Fuller trouve de nombreux usages en cartographie thématique. Voir par exemple cette carte originale des Décodeurs (Le Monde). Elle sert aussi pour re-projeter des cartes anciennes en dymaxion comme par exemple la carte d'Urbano Monte (site de David Rumsey)

On peut utiliser la projection Fuller aussi bien horizontalement que verticalement. Un usage pas du tout prévu à l'époque par son auteur : la projection Fuller peut être mieux vue sur l'écran vertical d'un téléphone portable qu'un planisphère classique à l'horizontal.
http://twitter.com/vid_jul/status/944117104122441728

Pour télécharger la projection Fuller en haute définition sur le site Map Porn :
http://www.reddit.com/r/MapPorn/comments/ex83s1/r_buckminster_fullers_dymaxion_projection/
 
Des projections Fuller à imprimer, découper et coller :
http://www.openstreetmap.org/user/smaprs/diary/39829

Souvent comparées, les projections Fuller et Waterman sont des projections polyédriques qui découpent le globe en triangles réguliers et réduisent les déformations. Elles ont pour point commun d'interrompre les continents et de brouiller nos repères traditionnels. Elles diffèrent cependant dans leur construction (lire le thread ci-dessous).









 
 





Ecrit par -